|
A follow-up to my post from a few weeks ago on Bellicum Pharmaceutical’s clinical trial hold, and the market’s (over)reaction. Yesterday, Bellicum issued an anodyne press release regarding discussions with the FDA on lifting the clinical hold on U.S. studies of BPX-501:
To address the FDA requirements, the Company plans to implement revisions to the U.S. study protocols, including the addition of more comprehensive monitoring and management of neurotoxicity. In addition, the Company will revise the Investigator Brochure and Informed Consent Documents to inform healthcare providers, patients and caregivers of the changes. Good news. Bellicum’s stock continued its recovery of the past month, $7.03 as of the Feb. 23 close, up from Jan. 31 opening price of $5.21. That’s a gain of 35% in less than a month, a very nice recovery indeed. The stock does remain 14% below the Jan 30. close of $8.20, however, a reminder of the investing truism that a 37% loss takes more than a 37% gain to recover initial value. Originally posted (on LinkedIn) 2018-02-24
0 Comments
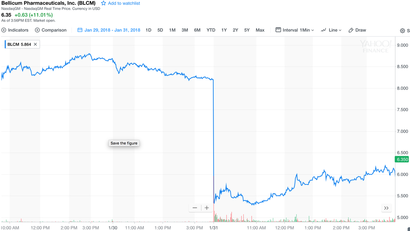 Bellicum Pharmaceuticals’ announced last week a clinical hold on its BPX-501 trials in the United States. On the face of it, things look bad: three patients (out of 240) developed “encephalopathy [an unspecified brain disorder or disease] deemed as possibly related to BPX-501.” One patient died; encephalopathy in the other two patients later resolved. Bellicum’s stock ($BLCM) duly tumbled 37% overnight, from $8.20 at close of trading on Jan. 30, to $5.17 when the market reopened the next day. The stock had already taken a beating over the past year, losing nearly half its value, in part due to significant concerns about Bellicum falling behind competitors Kite Pharma (now Gilead), Juno Therapeutics(Celgene acquisition closes 1Q2018), Bluebird Bio, and others in the genetically modified cell therapy arena. Market capitalizations (acquisition values) reiterate this story: Kite, ~$12 billion ; Juno, ~$10 billion; Bluebird, ~$9 billion; and Bellicum, ~$186 million. What is BPX-501, and where is it being tested? Bellicum is “developing novel stem cell transplant, TCR [T-cell receptor] and CAR [chimeric antigen receptor] T cell therapies,” such as BPX-501, that “incorporate molecular switches designed to allow activation or elimination of therapeutic cells once inside the body… the key to safer, more effective cell therapies.” BPX-501 may improve outcomes in patients undergoing haploidentical (partial match) hematopoietic stem cell transplants (HSCT). These patients suffer from various serious maladies, for example orphan inherited blood disorders (e.g. thalassemia) or hematologic malignancies, and HSCT—a procedure in which first diseased patient stem cells are eliminated, and then healthy donor stem cells are transplanted—can be curative. The procedure comes with significant risks, however, most notably life-threatening infections due to transient but profound immunosuppression, and acute or chronic graft-versus-host disease (GVHD), in which transplanted T cells (the graft) attack the host. GVHD clinical presentation is similar to, and in some cases can be hard to distinguish from, drug- or virus-induced Stevens–Johnson Syndrome, or the related, more severe Toxic Epidermal Necrolysis. GVHD mortality rates are about 20%. Bellicum’s procedure is to insert (“transduce”) into the donor stem cells’ genome DNA that expresses (FKBP12)-modified caspase-9—these modified cells are “BPX-501.” BPX-501 cells are then transplanted into a previously myeloablated patient. The magic of Bellicum’s protocol is that caspase-9 is inactive until it is “switched on,” only if and when needed, i.e. if GVHD rears its ugly head. The switch, rimiducid (AP1903), is a small molecule that binds to, dimerizes, and thereby activates the FKBP12–caspase-9, thus initiating apoptosis and elimination of the engrafted cells. If GVHD develops, rimiducid is administered; preliminary data indicate that this approach significantly improves outcomes. Pretty neat stuff! Except that one patient died, and two others got very ill. And the stock lost 37% of its value overnight. Common sense? Or overreaction? I vote overreaction. Most investors and analysts (but not all) seemed to fail to appreciate the great extent to which BPX-501 actually reduces the incidence of encephalopathy—even in the face of these three reported cases. In fact, central nervous system (CNS) complications of HSCT are common, and the incidence of “posterior reversible encephalopathy syndrome” (PRES) is about 7% at 180 days after transplantation (see Fig. 2 in above-cited reference). The Fig. 2survival data are fit pretty well by either exponential or Weibull (stretched exponential) models. Either way, the fits indicate a half-life to event (i.e., encephalopathy occurrence) of 16 to 19 days, with cumulatively ~7% of total patients at risk. Given this background, how many cases of encephalopathy should Bellicum have expected to see? Seven percent times 240 patients = 17 patients. And yet, they have only seen three cases—a clear improvement! Another way to approach these data is to ask, “What is the probability of observing only 3 events in a time period [180 days] during which 17 events typically should have been observed? We can use the Poisson distribution to answer this question, given that the underlying survival data are well-fitted by an exponential function, i.e. the average “time to event” is in fact time-independent. The Poisson probability, \(p\), of observing \(x\) events when on average \(\lambda\) events are expected — \[(x; \lambda) = e^{-\lambda}\lambda^x/x!, \text{for } x = 0, 1, 2, ⋯\] — is in this case \(p\)(3 observed; 17 expected) = \(3.4 \times 10^{-5}\), i.e. 0.000034; the cumulative probability of observing any of 0, 1, 2, or 3 events is about the same, 0.000041. In other words, vanishingly small—if, in fact, BPX-501 weren’t having a beneficial effect. Common sense? Or overreaction? You decide. David Borhani Originally posted (on LinkedIn) 2018-02-07 |
About DavidI grew up in Northern California. After studying chemistry at M.I.T. for 8 years (S.B.; Ph.D, with Fred Greene), I moved up the river to Harvard to learn structural biology with Steve Harrison. ArchivesCategories |
 RSS Feed
RSS Feed
